Lines That Intersect and Have Only One Point in Common

But here we assumed both l 1 l 2 pass through P Q. We proved that two intersecting lines determine a plane.

Two Lines In A Plane Either Intersect At Exactly One Point Or Are Parallel Youtube

The intersecting lines share a common point.

. This is because the lines intersect at asingle point. Parallel lines do not intersect at all. X 0 and y 0 which intersect just once x 0 and x 1 which intersect never x 0 and x 0 which i.

Now by Axiom 51 Given two distinct points there is a unique line that passes through them. For the time being let us suppose that the two lines intersect in two distinct points say P and Q. Lines that do not intersect at 90 Transitivity of Parallel Lines.

An angle that measures 90 Oblique lines. We need to prove that they have only one point in common. Intersecting lines have only one point in common a Line is a endless straight path and it haves a made up of a continuous collection of points.

If two lines are parallel to the same line then they are parallel to each other. The two non-parallel straight lines which are co-planar will have an intersection point. Vi A ray has one end point only.

I Two lines intersect in a point. If two parallel planes are cut by a third plane then the lines of intersection are parallel. See the answer See the answer See the answer done loading.

Answer 1 of 6. For instance one could have in the coordinate plane. We will prove this by contradiction.

By intersecting lines we mean the lines having one common point. Iii A segment has no length. Suppose there are two given lines l and m.

Yes the answer would be sometimes and not just for your reason. And this common point that exists on all intersecting lines is called the point of intersection. A line can intersect with and other line together forming into intersecting lines.

31 rows coplanar lines that have exactly one point in common. This means we have two lines passing through two distinct points P and Q. L 1 and l 2 cannot have more than 1 point in common Proof.

But this assumption clashes with the axiom that only one line can pass through two distinct points. Lines that intersect and have only one point in common are called _____. In progress 0 Mathematics Neala 3 months 2021-08-05T0416000000 2021-08-05T0416000000 2 Answers 2 views 0.

WA-5 College Geometry ABC and AGF have only point A in common ABC and EBF have only point B in common ABC and AED have only point A in common ABC and CFD have only point C in common ABC and BGD have only point B in common ABC and CGE have. Intersect each other at a unique point. Lines that intersect to form 90 angles are called _____.

Let us suppose that the two lines intersect in two distinct points say A and B. So intersecting lines are always coplanar lines. Prove that if two distinct lines intersect then they have only one point in common This problem has been solved.

Ii Two lines may intersect in two points. Two distinct lines cannot have more than one point in common. The x a y b isthe one and only solution for the system.

V Every ray has a finite length. Ix Only a single line may pass through a given point. Let l 1 l 2 have two points in common P Q.

Kenneth M Jones Jr. Vii A segment has one end point only. We need to prove that they have only one point in common.

That means they have only one point in common. L1 Lines that lie on top of one another and have all points in common are called _____ lines. A system of equations will have one solution if the graphs ofthe lines intersect.

Lines that intersect at right angles. Viii The ray AB is same as ray BA. The statement is true because any 2 lines intersect at only one point because of.

IvTwo distinct points always determine a line. Up to 24 cash back -In my picture it is important that the lines intersect because they are train tracks and by them intersecting the trains that travel on the tracks are able to go many different ways like they are able to turn or keep staright just by these lines intersecting. Two nonvertical lines are perpendicular if and.

Thus only one line passes through two distinct points P Q. By the axiom we have mentioned in our answer there exists only one line linexy through x and y. So you have two lines passing through two distinct points P and Q.

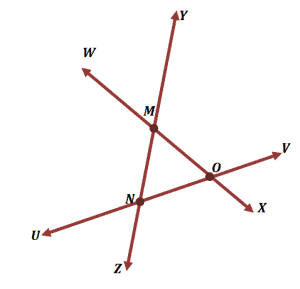
Here lines A and B intersect at point O which is the point of intersection. Well what do u think. To Prove.

Up to 25 cash back Assume that lineAB and lineCD are different but that there are points x and y such that x y is contained in lineAB and xy is contained in lineCD ie lineAB n lineCD x y. A line that intersects two coplanar lines at two different points is called a _____. Lets say that point is a b.

L1 Pairs of angles formed when a transversal intersects two lines so that they lie on the same side of the transversal and on the same sides of the lines are called _____. True Parallel lines are defined as lines that have only one point in common. Lines that intersect and have only one point in common are called _____.

Intersecting Lines Properties Examples Meaning

Intersecting Lines Explanations Examples

Intersecting Lines Explanations Examples